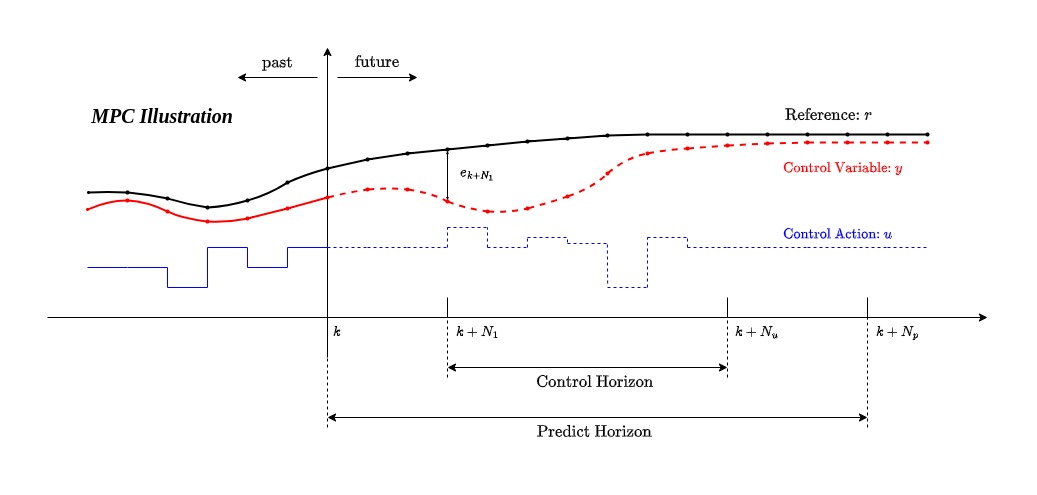
Model Predictive Control Part 1. Generized Problem Setup

In this post, we propose a generalized approach for modeling MPC problems for non-linear system.

Linearization

Consider a non-linear continuous system

\[\dot{x} = f(x,u)\]

using first order taylor expansion to linearize

\[\dot{x} = \left.\frac{\partial f}{\partial x}\right \vert_{(\hat{x},u_0)}(x-\hat{x})+\left.\frac{\partial f}{\partial u}\right \vert_{(\hat{x},u_0)}(u-u_0)+f(\hat{x},u_0)\]

define

\[\begin{aligned} A &= \left.\frac{\partial f}{\partial x}\right \vert_{(\hat{x},u_0)} \\ B &= \left.\frac{\partial f}{\partial u}\right \vert_{(\hat{x},u_0)} \\ \dot{\hat{x}} &= f(\hat{x},u_0) \end{aligned}\]

rewrite system in error space, we have

\[\begin{aligned} \dot{x} &=&& \left.\frac{\partial f}{\partial x}\right \vert_{(\hat{x},u_0)}(x-\hat{x})+\left.\frac{\partial f}{\partial u}\right \vert_{(\hat{x},u_0)}(u-u_0)+f(\hat{x},u_0)\\ &=&& A(x-\hat{x}) + B(u-u_0) + \dot{\hat{x}} \end{aligned}\]

Discretization

Assumptions:

• constant control $u$ at time interval $[kh \quad kh+h)$
• fix expansion point $(\hat{x},u_0)$ at time interval $[kh \quad kh+h)$
• constant system matrix pair $(A,B)$ (LTI system) at time interval $[kh \quad kh+h)$

Next, we start with auxiliary matrix function $K(t) = e^{-At}$

\[\begin{aligned} &\frac{d}{dt}[e^{-At}(x-\hat{x})] = -e^{-At}A(x-\hat{x})+e^{-At}(\dot{x} - \dot{\hat{x}}) \\ &\frac{d}{dt}[e^{-At}(x-\hat{x})] + e^{-At}A(x-\hat{x}) = e^{-At}(\dot{x} - \dot{\hat{x}}) \\ \end{aligned}\]

expand RHS with error space system

\[\begin{aligned} e^{-At}(\dot{x} - \dot{\hat{x}}) &= e^{-At}(A(x-\hat{x})+B(u-u_0)) \\ &= e^{-At}A(x-\hat{x})+e^{-At}B(u-u_0)\\ &= e^{-At}A(x-\hat{x}) + \frac{d}{dt}[e^{-At}(x-\hat{x})] \end{aligned}\]

thus, we have

\[\frac{d}{dt}[e^{-At}(x-\hat{x})] = e^{-At}B(u-u_0)\]

Take integral at both side

\[\begin{aligned} \int_{kh}^{kh+h} \frac{d}{dt}[e^{-At}(x-\hat{x})] dt &= \int_{kh}^{kh+h}e^{-At}B(u-u_0)dt\\ e^{-At}(x-\hat{x})\vert_{kh}^{kh+h} &= \int_{kh}^{kh+h}e^{-At}B(u-u_0)dt\\ e^{-A(kh+h)}(x(kh+h)-\hat{x}(kh+h))- e^{-Akh}(x(kh)-\hat{x}(kh))&= \int_{kh}^{kh+h}e^{-At}B(u-u_0)dt\\ \end{aligned}\] \[\begin{aligned} x(kh+h)-\hat{x}(kh+h)&= e^{A(kh+h)}[e^{-Akh}(x(kh)-\hat{x}(kh)) + \int_{kh}^{kh+h}e^{-At}B(u-u_0)dt]\\ &=e^{Ah}(x(kh)-\hat{x}(kh))+\int_{kh}^{kh+h}e^{A(kh+h-t)}B(u-u_0)dt\\ &=e^{Ah}(x(kh)-\hat{x}(kh))+\int_{kh}^{kh+h}e^{A(kh+h-t)}dtB(u(kh)-u_0)\\ \end{aligned}\]

let

\[\begin{aligned} v &= kh+h-t \\ t &= kh, v =h\\ t &= kh+h, v = 0\\ dv &= -dt \end{aligned}\]

subs in, we have

\[\begin{aligned} x(kh+h)-\hat{x}(kh+h)&=e^{Ah}(x(kh)-\hat{x}(kh))+\int_{kh}^{kh+h}e^{A(kh+h-t)}dtB(u(kh)-u_0)\\ &=e^{Ah}(x(kh)-\hat{x}(kh))-\int_{h}^{0}e^{Av}dvB(u(kh)-u_0)\\ &=\underbrace{e^{Ah}}_{\approx A_d}(x(kh)-\hat{x}(kh))+\underbrace{\int_{0}^{h}e^{Av}dvB}_{\approx B_d}(u(kh)-u_0)\\ &\approx A_d(x(kh)-\hat{x}(kh))+Bd(u(kh)-u_0) \end{aligned}\]

Define $x(k) = x(kh),\hat{x}(k) = \hat{x}(kh)$

\[x(k+1) = A_dx(k)+B_du(k)+ \hat{x}(k+1) -A_d \hat{x}(k)- B_du_0\]

Define residue $\delta(k)$ as

\[\delta(k) = \hat{x}(k+1) - A_d \hat{x}(k)- B_du_0\]

thus

\[x(k+1) = A_dx(k)+B_du(k)+ \delta(k)\]

Cost Function

Cost $J_1$ : state deviation, where $Q$ is a semi-positive definite matrix

\[\begin{aligned} J_1 &= \frac{1}{2}||x-x_{ref}||_{Q} \\ &= \frac{1}{2}\sum_{k=0}^N(x(k)-x_{ref}(k))^TQ(k)(x(k)-x_{ref}(k))\\ &= \frac{1}{2}\sum_{k=0}^Nx(k)^TQ(k)x(k)-2(Q(k)x_{ref}(k))^Tx(k) + x_{ref}(k)^TQ(k)x_{ref}(k)\\ \end{aligned}\]

Cost $J_2$: control deviation, where $S$ is a semi-positive definite matrix

\[\begin{aligned} J_2 &= \frac{1}{2}||u-u_{ref}||_{S} \\ &= \frac{1}{2}\sum_{k=0}^{N-1}(u(k)-u_{ref}(k))^TS(k)(u(k)-u_{ref}(k))\\ &= \frac{1}{2}\sum_{k=0}^{N-1}u(k)^TS(k)u(k)-2(S(k)u_{ref}(k))^Tu(k) + u_{ref}(k)^TS(k)u_{ref}(k)\\ \end{aligned}\]

Cost $J_3$: control smoothness,where $R$ is a semi-positive definite matrix

\[\begin{aligned} J_3 &= \frac{1}{2}||\Delta u||_{R} \\ &= \frac{1}{2}\sum_{k=0}^{N-1}\Delta u^TR\Delta u \\ \end{aligned}\]

Total cost $J$ is

\[\begin{aligned} J &=&& J_1 + J_2 + J_3\\ &=&& \frac{1}{2} [\sum_{k=0}^Nx(k)^TQ(k)x(k)-2(Q(k)x_{ref}(k))^Tx(k) + x_{ref}(k)^TQ(k)x_{ref}(k) + \\ &&&\quad\sum_{k=0}^{N-1}u(k)^TS(k)u(k)-2(S(k)u_{ref}(k))^Tu(k) + u_{ref}(k)^TS(k)u_{ref}(k) +\\ &&&\quad\sum_{k=0}^{N-1}\Delta u^TR\Delta u ] \end{aligned}\] \[\begin{aligned} \mathop{\arg \min}\limits_{x,u,\Delta u} J &=&& \mathop{\arg \min}\limits_{x,u,\Delta u}(J_1 + J_2 + J_3)\\ &=&& \mathop{\arg \min}\limits_{x,u,\Delta u}\frac{1}{2} [\sum_{k=0}^Nx(k)^TQ(k)x(k)-2(Q(k)x_{ref}(k))^Tx(k) + x_{ref}(k)^TQ(k)x_{ref}(k) + \\ &&&\qquad\qquad\ \sum_{k=0}^{N-1}u(k)^TS(k)u(k)-2(S(k)u_{ref}(k))^Tu(k) + u_{ref}(k)^TS(k)u_{ref}(k) +\\ &&&\qquad\qquad\ \sum_{k=0}^{N-1}\Delta u^TR\Delta u ]\\ &=&& \mathop{\arg \min}\limits_{x,u,\Delta u}\frac{1}{2} [\sum_{k=0}^Nx(k)^TQ(k)x(k)-2(Q(k)x_{ref}(k))^Tx(k) + \\ &&&\qquad\qquad\ \sum_{k=0}^{N-1}u(k)^TS(k)u(k)-2(S(k)u_{ref}(k))^Tu(k) + \\ &&&\qquad\qquad\ \sum_{k=0}^{N-1}\Delta u^TR\Delta u ] \\ &=&&\mathop{\arg \min}\limits_{x,u,\Delta u} J^* \end{aligned}\]

define decision variable $\xi$ as

\[\begin{aligned} \xi = \begin{bmatrix} x(0)\\ x(1) \\ \vdots \\x(N) \\ u(-1) \\ u(0) \\u(1)\\\vdots\\u(N-1)\\ \Delta u(-1)\\ \Delta u(0) \\ \Delta u(1) \\ \vdots \\\Delta u(N-1)\\\delta(-1) \\ \delta(0) \\\cdots \\\delta(N-1)\end{bmatrix} \end{aligned}\] \[\xi \in \Re^{((N+1)n_s + (N+1)n_c + *(N+1)n_c +(N+1)n_c)\times1 }=\Re^{N_p\times1 }\]

rewrite the optimization problem with decision variable

\[\begin{aligned} \mathop{\arg \min}\limits_{x,u,\delta u} J^* &= \mathop{\arg \min}\limits_{x,u,\delta u}\frac{1}{2} \xi ^T diag \begin{pmatrix}Q(0)& Q(1)&\cdots & Q(N)&0&S(0)&S(1)&\cdots&S(N-1)&0&R(0)&R(1)&\cdots&R(N-1)& 0 &0& \cdots & 0\end{pmatrix} \xi\\ &+ \begin{bmatrix}-Q(0)x_{ref}(0) & -Q(1)x_{ref}(1) & \cdots & -Q(N)x_{ref}(N) & 0 & -S(0)u_{ref}(0) & -S(1)u_{ref}(1) & \cdots & -S(N-1)u_{ref}(N-1) & 0 &\cdots & 0 & 0 &\cdots & 0\end{bmatrix} \xi \end{aligned}\]

Define hessian matrix $P$ and gradient matrix $q$ as

\[\begin{aligned} P &= diag( \underbrace{Q(0)\quad Q(1)\quad\cdots \quad Q(N)}_{(N+1)\times(n_s \times n_s)}\quad \underbrace{0\quad S(0)\quad S(1)\quad \cdots\quad S(N-1)}_{(N+1)\times(n_c \times n_c)}\quad \underbrace{0\quad R(0)\quad R(1)\quad\cdots\quad R(N-1)}_{(N+1)\times(n_c \times n_c)}\quad \underbrace{0\quad 0\quad \cdots \quad 0}_{(N+1)\times(n_s \times n_s)} )\\ q &=[ \underbrace{-x_{ref}^T(0)Q(0)\quad -x_{ref}^T(1)Q(1) \quad \cdots \quad -x_{ref}^T(N)Q(N)}_{(N+1)\times(1 \times n_s)} \quad \underbrace{ 0 \quad -u_{ref}^T(0)S(0) \quad -u_{ref}^T(1)S(1) \quad \cdots \quad -u_{ref}^T(N-1) S(N-1)}_{(N+1)\times(1 \times n_c)}\quad \underbrace{0 \quad \cdots \quad 0}_{(N+1)\times(1 \times n_c)}\quad \underbrace{0 \quad \cdots \quad 0}_{(N+1)\times(1 \times n_s)}]^T \end{aligned}\]

rewrite the cost function, we have

\[\mathop{\arg \min}\limits_{\xi} J^* =\mathop{\arg \min}\limits_{\xi}\frac{1}{2} \xi ^T P \xi +q^T\xi\]

Constraint

initial condition constraint

\[\begin{aligned} x(0) &= x(0) (known) \\ u(-1) &= u(-1) (known) \\ \Delta u(-1) &= 0 \\ \delta(-1) &= 0 \end{aligned}\]

system constraint

\[\begin{aligned} x(1) &= A_d(0)x(0)+B_d(0)u(0)+ \delta(0) \\ x(2) &= A(1)_dx(1)+B_d(1)u(1)+ \delta(1) \\ &\vdots \\ x(k+1) &= A_d(k)x(k)+B_d(k)u(k)+ \delta(k) \\ &\vdots \\ x(N) &= A_d(N-1)x(N-1)+B_d(N-1)u(N-1)+ \delta(N-1) \\ \\\\ u(0) &= u(-1) + \Delta u(0)\\ u(1) &= u(0) + \Delta u(1)\\ &\vdots \\ u(k) &= u(k-1) + \Delta u(k)\\ &\vdots \\ u(N-1) &= u(N-2) + \Delta u(N-1) \end{aligned}\]

equivalently

\[\begin{aligned} 0 &= A_d(0)x(0) - x(1)+B_d(0)u(0)+ \delta(0) \\ 0 &= A_d(1)x(1) - x(2)+B_d(1)u(1)+ \delta(1) \\ &\vdots &\\ 0 &= A_dx(k) - x(k+1)+B_du(k)+ \delta(k) \\ &\vdots &\\ 0 &= A_d(N-1)x(N-1) - x(N)+B_d(N-1)u(N-1)+ \delta(N-1) \\ \\\\ 0 &= u(-1) - u(0) + \Delta u(0)\\ 0 &= u(0) - u(1)+ \Delta u(1)\\ &\vdots &\\ 0 &= u(k-1) -u(k)+ \Delta u(k)\\ &\vdots &\\ 0 &= u(N-2)-u(N-1) + \Delta u(N-1) \end{aligned}\]

state constraint

\[x_{min}(k)\leq x(k) \leq x_{max}(k)\]

control constraint

\[u_{min}(k)\leq u(k) \leq u_{max}(k)\]

control rate constraint

\[\Delta u_{min}(k)\leq \Delta u(k) \leq \Delta u_{max}(k)\]

total constraint matrix

\[\underbrace{\begin{bmatrix} -x(0)\\ 0\\ 0\\ \vdots\\ 0\\ 0\\ 0\\ 0\\ \vdots\\ 0\\ x_{min}(0)\\ x_{min}(1)\\ x_{min}(2)\\ \vdots\\ x_{min}(N)\\ u(-1)\\ u_{min}(0)\\ u_{min}(1)\\ \vdots\\ u_{min}(N-1)\\ 0\\ \Delta u_{min}(0)\\ \Delta u_{min}(1)\\ \vdots\\ \Delta u_{min}(N-1)\\ 0\\ \delta(0)\\ \delta(1)\\ \vdots\\ \delta(N-1)\\ \end{bmatrix}}_{l_{\xi}} \leq \underbrace{ \begin{bmatrix} -I & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & I & 0 & 0 & \cdots & 0 \\ A_d(0)& -I & 0 & \cdots & 0 & 0 & B_d(0) & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & I & 0 & \cdots & 0\\ 0& A_d(1) & -I & \cdots & 0 & 0 & 0 & B_d(1) & \cdots & 0 & 0 & 0 & 0 & \cdots &0 & 0 & 0 & I & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & -I & 0 & 0 & 0 & \cdots & B_d(N-1) & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & I\\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & I & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & \cdots & 0 & I & -I & 0 & \cdots & 0 & 0 & I & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & \cdots & 0 & 0 & I & -I & \cdots & 0 & 0 & 0 & I & \cdots & 0 & 0 & 0 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & -I & 0 & 0 & 0 & \cdots & I & 0 & 0 & 0 & \cdots & 0 \\ I & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & I & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0\\ 0 & 0 & I & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0\\ \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots &\vdots& \vdots & \vdots & \ddots & \vdots &\vdots& \vdots & \vdots & \ddots & \vdots & \\ 0 & 0 & 0 & \cdots & I & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & I & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & I & & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & I & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & I & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & I & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & I & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & I & \cdots & 0 &0 & 0 & 0 & \cdots & 0 \\ \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & I &0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &I & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & I & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & I & \cdots & 0 \\ \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \vdots& \vdots & \vdots & \ddots & \vdots & \\ 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 &0 & 0 & 0 & \cdots & I \\ \end{bmatrix}}_{A_c} \begin{bmatrix} x(0)\\ x(1) \\ x(2) \\ \vdots \\x(N) \\ u(-1) \\ u(0) \\u(1)\\\vdots\\u(N-1)\\ \Delta u(-1)\\ \Delta u(0) \\ \Delta u(1) \\ \vdots \\\Delta u(N-1)\\\delta(-1) \\ \delta(0) \\ \delta(1) \\\cdots \\\delta(N-1)\end{bmatrix} \leq \underbrace{ \begin{bmatrix} -x(0)\\ 0\\ 0\\ \vdots\\ 0\\ 0\\ 0\\ 0\\ \vdots\\ 0\\ x_{max}(0)\\ x_{max}(1)\\ x_{max}(2)\\ \vdots\\ x_{max}(N)\\ u(-1)\\ u_{max}(0)\\ u_{max}(1)\\ \vdots\\ u_{max}(N-1)\\ 0\\ \Delta u_{max}(0)\\ \Delta u_{max}(1)\\ \vdots\\ \Delta u_{max}(N-1)\\ 0\\ \delta(0)\\ \delta(1)\\ \vdots\\ \delta(N-1)\\ \end{bmatrix}}_{u_{\xi}}\]

The constraints could be written in compact form:

\[\begin{aligned} &l_{\xi} \leq A_c \xi \leq u_{\xi} \\\\ &A_c \in \Re^{N_c \times N_p}\\ &\xi \in \Re^{((N+1)n_s + (N+1)n_c + (N+1)n_c +(N+1)n_c)\times1 }=\Re^{N_p\times1 }\\ &l_{\xi},u_{\xi} \in \Re^{((N+1)n_s + (N+1)n_c + (N+1)n_s +(N+1)n_c + (N+1)n_c + (N+1)n_s)\times1 }=\Re^{N_c\times1} \end{aligned}\]

Problem Setup

The model predictive control problem could be written in compact form:

\[\begin{aligned} \mathop{\arg \min}\limits_{\xi}\frac{1}{2} \xi ^T P \xi +q^T\xi \\ s.t. \qquad l_{\xi} \leq A_c \xi \leq u_{\xi} \end{aligned}\]