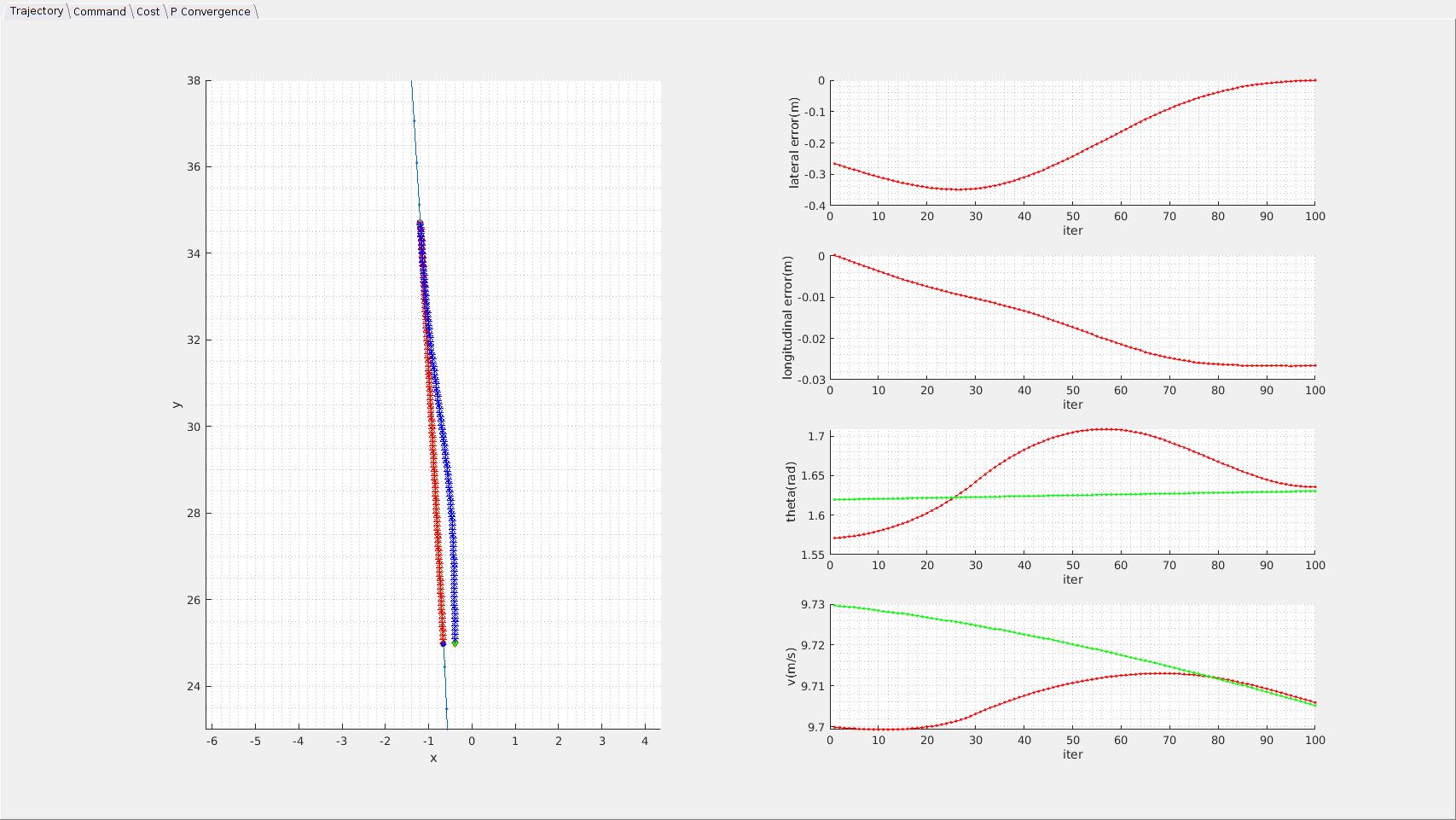
Trajectory Smoothing
Error State Incremental Trajectory Model Derivation Starting with a time-varying non-linear trajectory dynamics [\dot{x} = f(t,x,u)] Recall the linearization section described in lqr post, the co...

Error State Incremental Trajectory Model Derivation Starting with a time-varying non-linear trajectory dynamics [\dot{x} = f(t,x,u)] Recall the linearization section described in lqr post, the co...
Motivation Tracking a desired trajectory while minimizing a quadratic cost function is a critical problem in many engineering and scientific domains. However, solving this problem analytically can...
In this post, we demonstrate a basic design process of Lateral Stanley Controller with time domain and frequency domain specifications. Plant Model The front axle based error state vehicle lateral...
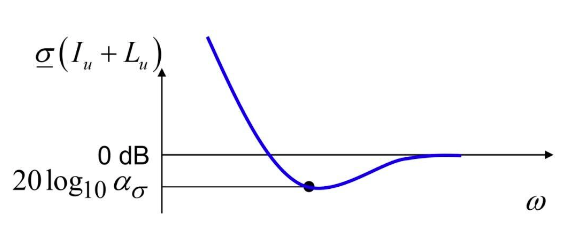
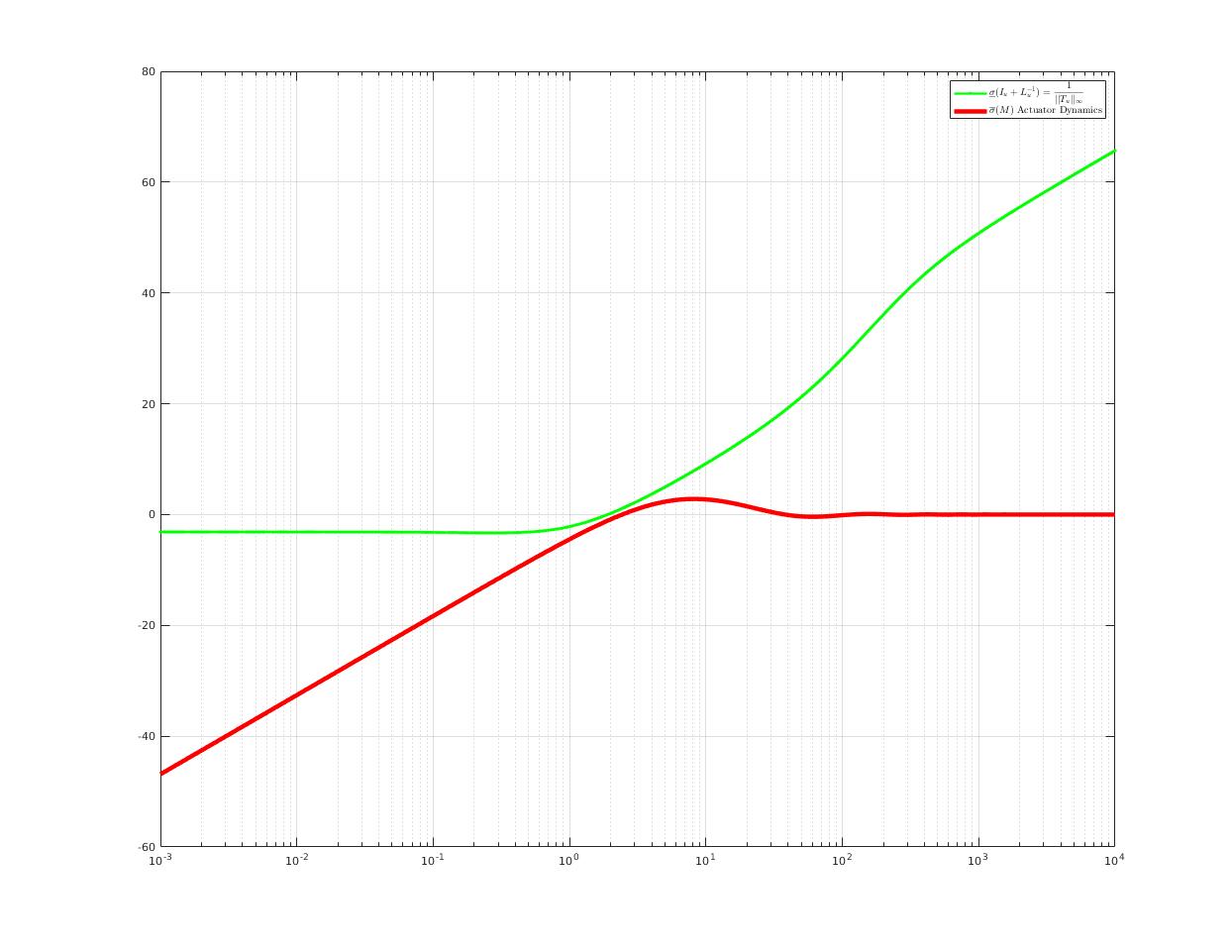
Good stability margins do not imply robustness, must look at distance to (-1,0)! Motivation Multi-variable Nyquist Theorem only determines absolute stability of a system, it does not indicate...
In this post, we show how to analysis robustness of a MIMO system with Multi-variable Nyquist Theorem. Determinant of Return Difference The determinant of return difference matrix could be expres...
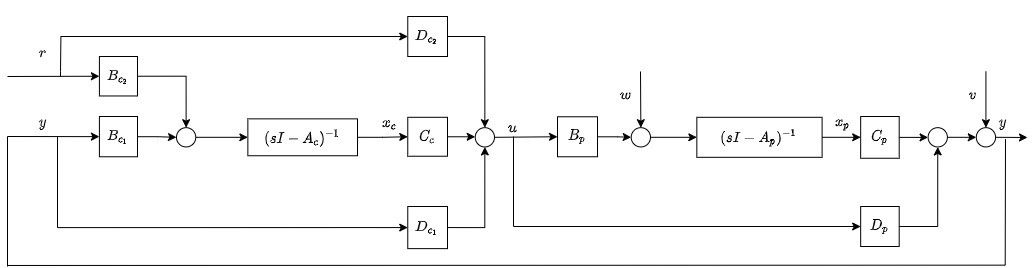
In this post, we present a generalized state-space linear-time-invariant plant and controller models for control design and frequency domain analysis that will be used in other sections. Models fo...
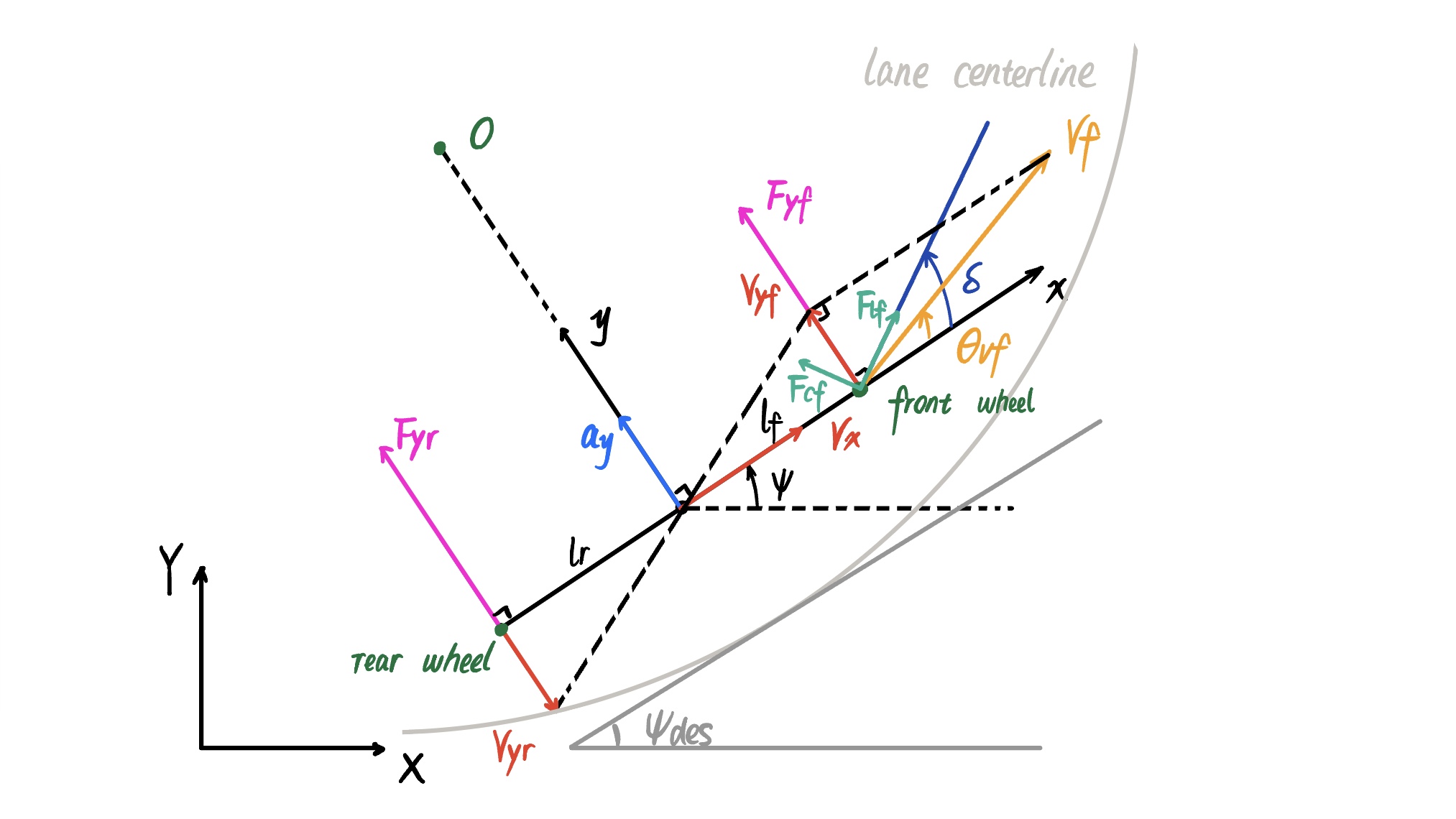
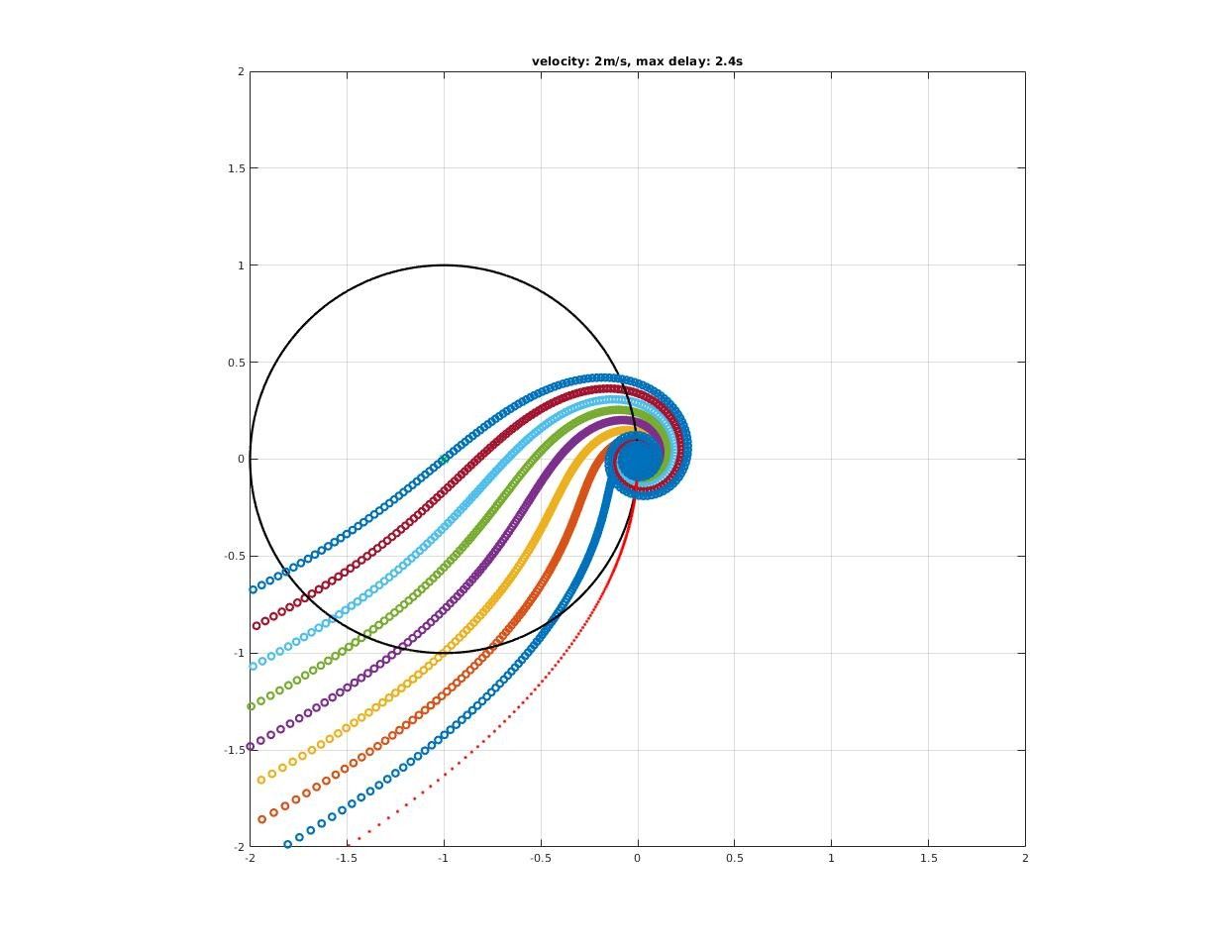
Motivation First of all, we must ask: Why do we need to establish a dynamic model for vehicle lateral control? Simply put, when a vehicle operates at higher speeds, the assumption in kinematic mod...
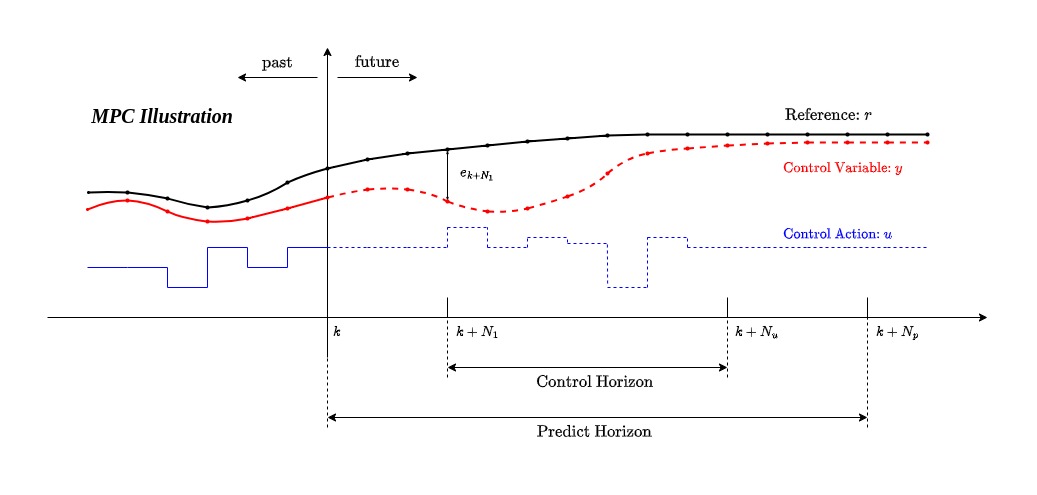
In this post, we propose a generalized approach for modeling MPC problems for non-linear system. Linearization Consider a non-linear continuous system [\dot{x} = f(x,u)] using first order taylo...
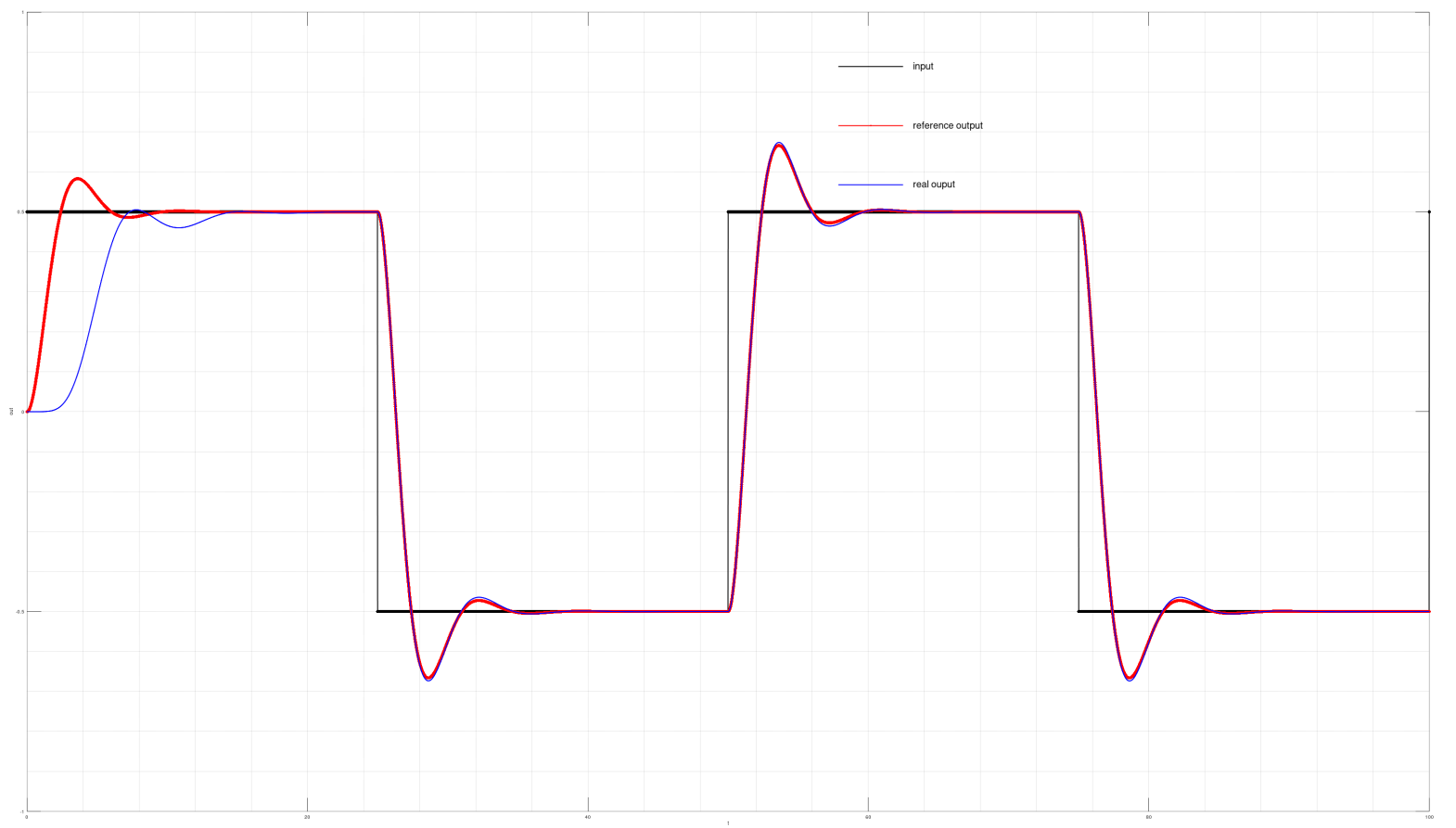
Motivation In the design of vehicle control system, it is essential to provide closed-loop stability, adequate command tracking performance, as well as robustness to model uncertainties, control f...